Riding the Bézier wave

When working on 2D/3D graphic applications, animating various objects and moving them across the screen is very often a requirement. As a programmer or designer, sometimes you would like to have the freedom to move objects not only along straight, but also along curved lines. Solution to this problem Рthe B̩zier curve Рhas been known for decades. Still, people unfamiliar with curves may find them a bit confusing at first. This article is not intended to be a comprehensive analysis of B̩zier curves; rather, it should give a beginner just enough knowledge to get her/him started.

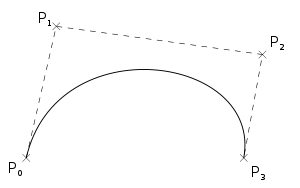
For now, we’ll focus on cubic Béziers – they provide enough control over the curve and are simple to calculate at the same time. Every cubic curve is defined by four control points: P₀(x₀, y₀), P(x₁, y₁), P₂(x₂, y₂) and P₃(x₃, y₃). P₀ is the start point, P₃ is the end point. The curve passes through P₀ and P₃, but not through P₁ and P₂. All points on the curve are defined with:

C(p) = ∑ Pi Bi,n(p)		i∈[0,n]

Note that this expands to two equations – one for x, and one for y coordinate. Since the curve is cubic, n = 3:

Cx(p) = ∑ Pxi Bi,3(p)
Cy(p) = ∑ Pyi Bi,3(p)

In each equation, B_i,3 is one Bernstein polynomial. Bernstein polynomials have all kinds of nice properties – but we’re currently not interested in them, so we’ll just write down all four polynomials of third degree:

b0,3(p) = (1 - p)3
b1,3(p) = 3p (1 - p)2
b2,3(p) = 3p2 (1 - p)
b3,3(p) = p3

So, what exactly is going on? Parameter p gradually changes from 0 to 1. For each value of p, we evaluate the polynomials, then multiply each polynomial with the coordinate of its corresponding control point. Finally, we add all these values to obtain the x coordinate of curve point at p:

Cx(p) = ∑ Pxi Bi,n(p)
      = x0 b0,3(p) + x1 b1,3(p) + x2 b2,3(p) + x3 b3,3(p)

Calculating the y coordinate is the same, except that y coordinates of control points are used instead of x. To speed things up, previous equation can be expanded, and the terms rearranged:

Cx(p) = ax p3 + bx p2 + cx p + dx        (*)

where:

ax = x3 - 3x2 + 3x1 - x0
bx = 3x2 - 6x1 + 3x0
cx = 3x1 - 3x0
dx = x0

Now, as soon as you are given four control points, you can calculate a_x, b_x, c_x and d_x. After that, all you have to do is vary the value of p from 0 to 1, and use it to evaluate (*). Then, repeat the procedure for y coordinates. Smaller changes of p will result in more calculations, but the curve will appear smoother. And that’s all there is to it.